H27 問03

＜画像クリックで拡大表示＞
問題はこちら

解説

磁化特性に関する問題です。
つまりは、ヒステリシス曲線のことです。

問題のグラフだけだと、初めて見るグラフだと思う方もいるかもしれませんが、
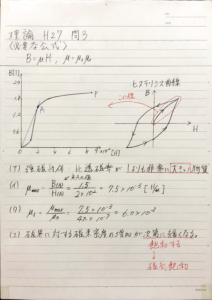
このグラフはヒステリシス曲線の一部です。どの部分を指しているかは添付画像を参照ください。

透磁率は\(\mu=\frac{B}{H}\)で導出されます。
しかもこのグラフからわかるように、\(B\)と\(H\)は比例関係ではありません。
\(H\)を大きくしていくと、\(B\)は変化しにくくなります。これを磁気飽和といいます。

電験の学習とはあまり関係ないのですが、
実は透磁率\(\mu\)や誘電率\(\varepsilon\)は材料によって決まる物性値ですが、
いつでも決まった値を示すものではありません。
誘電率\(\varepsilon\)は電界の変化速度（周波数）が高くなると変化しますし、
透磁率\(\mu\)は磁界の変化速度（周波数）だけでなく、磁界の強さでも変化します。

電気回路で扱う周波数帯域で登場する誘電率\(\mu\)や透磁率\(\varepsilon\)と、
光の領域（光も電磁波なので）で登場する誘電率\(\mu\)や透磁率\(\varepsilon\)では、
物性値としての役割が変わってくるということを知っておくといいことがあるかもしれません。
（こういうこと書いてある参考書少ないので、コメントさせていただきました）

さて前置きが長くなりましたが、（イ）の透磁率の最大値を求めます。
具体的な指示はありませんが、グラフの傾きが大きい部分の最終値（添付画像のグラフの点A）と
原点を結ぶ直線の変化の割合を最大値とするのがよいと思います。
$$\mu_{max}=\frac{B(A)}{H(A)}=\frac{1.5}{2\times 10^2}=7.5\times 10^{-3} \,\rm{H/m}$$

比透磁率\(\mu_r\)は先に求めた透磁率\(\mu_{max}\)を真空の透磁率\(\mu_0\)で割ったものになります。
$$\mu_r=\frac{\mu_{max}}{\mu_0}=\frac{7.5\times 10^{-3}}{4\pi\times10^{-7}}=6.0\times10^{3}\,\rm{H/m}$$

ヒステリシス曲線の理解を深めるいい問題ですので、苦手な方はこの問題をきちんと押さえておきましょう。