H27 問17

＜画像クリックで拡大表示＞
問題はこちら

解説

三相交流に関する問題です。

Ｖ結線について問題となります。
（私のように）苦手なかたは問題を通じて理解を深めましょう。

Ｖ結線とは

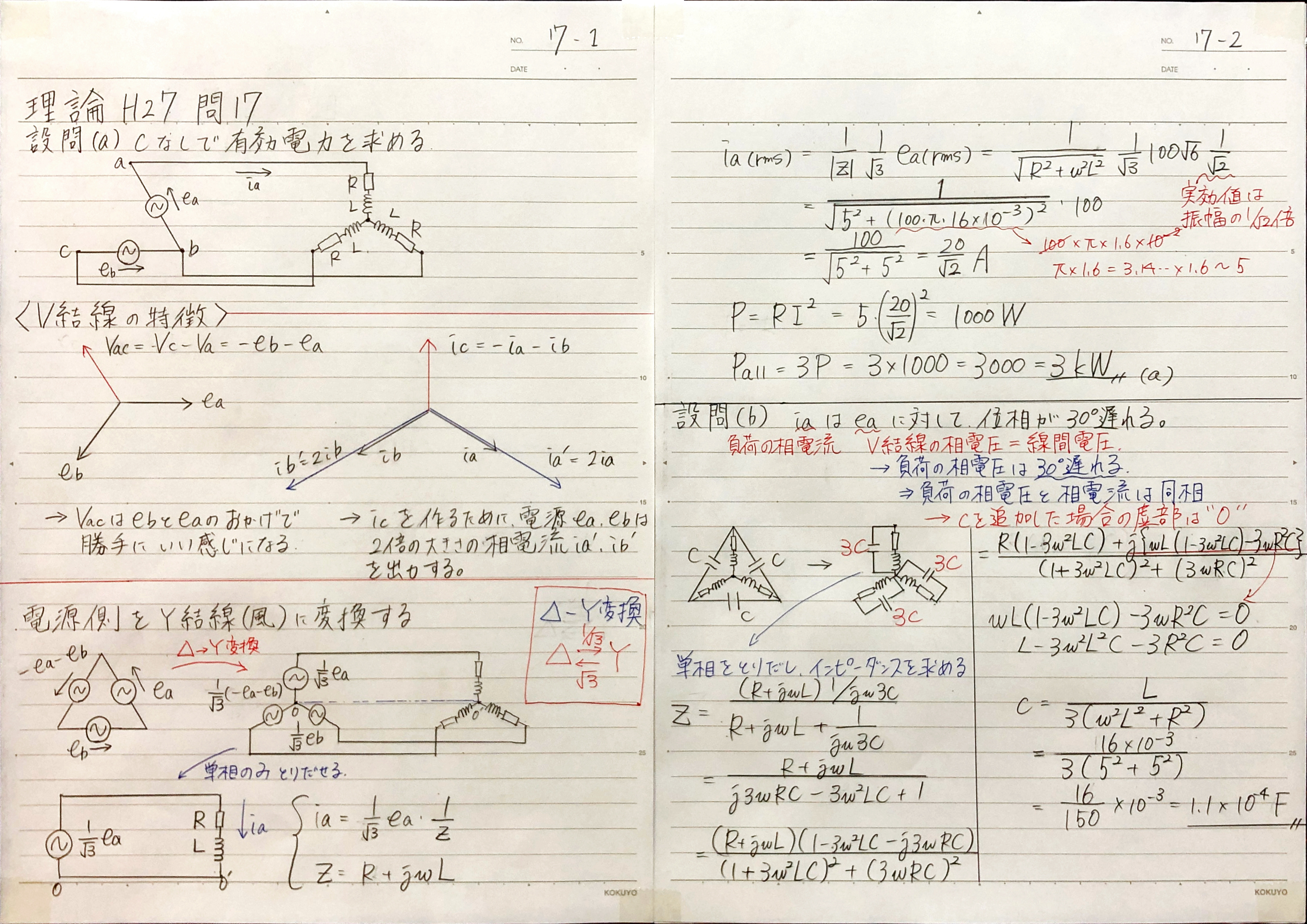
添付画像の左ページの中央部にＶ結線の特徴を記載しました。
電源が2個しかないですが、電圧はデルタ結線と同じように、１２０°位相がずれた三相の電圧を供給することができます。
一方電流は2個の電源で帳尻を合わせる必要があるので、2個の電源が通常の三相交流回路よりも多めに電流を出力をします。

その結果、少し燃費の悪い（効率の低い）デルタ結線としてＶ結線は働くことになります。

設問（ａ）

Ｖ結線はデルタ結線と思って計算を進めて構いません。
ということで、まずは電源のデルタースター変換を行います。

三相交流の計算ではとにかくスター結線に変換することが最初の一手です。
スター結線に変換すると、単相交流の回路に分解ができるので、計算が非常にシンプルになります。

問題でデルタ結線の指定があれば、計算結果はデルタ結線に再度変換しないといけないので、
デルタ結線とスター結線を相互に行き来できるように訓練が必要になります。

デルタースター変換では電源電圧は\(1/\sqrt{3}\)倍になるということを覚えておきましょう。

変換した回路と取り出した単相の回路が添付画像の左ページの下部の図になります。

問題では有効電力（単位がkWなので）を導出する必要があるので、まず負荷の電流を求めます。

負荷のインピーダンスは抵抗とコイルが接続されています。
有効電力を求めるためには電流の大きさが分かればいいので、位相のことは一旦忘れて、
インピーダンスの絶対値（大きさ）のみを考えます。

また、問題で電源電圧が以下のように表されています。
$$e_a=100\sqrt{6}\sin(100\pi t)$$
位相のことは一旦忘れると言っているので、\(\sin(100\pi t)\)の部分は無視してかまいません。
\(e_a=100\sqrt{6}\)として扱いましょう。

ここでスター結線に変換されているので\(e_a\)の大きさは\(1/\sqrt 3\)倍され、
さらに実効値を扱うので振幅の\(1/\sqrt{2}\)倍を考えます。
ということで、以上のことを踏まえて、負荷電流\(i_a\)の立式を行います。
$$i_a=\frac{1}{|z|}\frac{1}{\sqrt 3}e_{a(rms)}=\frac{1}{\sqrt{R^2+\omega^2L^2}} \frac{1}{\sqrt 3}\frac{1}{\sqrt{2}}100\sqrt 6$$
$$i_a=\frac{1}{\sqrt{5^2+(100\pi\cdot 16\times 10^{-3})^2}}\cdot 100\sim \frac{20}{\sqrt 2}$$

電流が分かったので、単相分の有効電力を求めます。
$$P=RI^2=5\cdot\left(\frac{20}{\sqrt 2}\right)^2=1000\,\,\rm W$$
三相分の電力にするには\(Ｐ\)を3倍します。
$$P_{all}=3P=3000\,\,\rm W=3\,\,\rm{kW}$$

設問（ｂ）

次はコンデンサを負荷に接続し、そのときのコンデンサの静電容量を求めます。

問題より、「\(i_a\)の波形は\(e_a\)の波形に対して位相が30°遅れていた」という記述があります。

この条件を満たすように静電容量を求めればいいことになります。

ここで、再び添付画像の左ページ中央部の「Ｖ結線の特徴」の図を見てみましょう。
電圧\(e_a\)のベクトルは電流\(i_a\)のベクトルよりも30°遅れていることが分かります。

負荷で位相差が発生しなければ、この電圧と電流の位相関係は保持されます。
すなわち、この問題ではコンデンサを追加することで、負荷で発生する位相差が打ち消されるということを表しています。

ということで、コンデンサを加えた負荷の合成インピーダンスを求め、虚部が0となる静電容量を求めればいいことになります。

さっそく、合成インピーダンスの計算に移りたいのですが、
一呼吸おいてデルタ結線になっているコンデンサの接続をまずスター結線に変換します。

コンデンサのデルタースター変換では各相の静電容量は3倍となります。（添付画像の右ページ中央部の図を参照下さい）

以上でインピーダンスを求める準備ができたので計算に移ります。
$$z=\frac{(R+j\omega L)\cdot 1/j\omega 3C}{R+j\omega L+1/j\omega 3C}=\frac{R+j\omega L}{j3\omega RC-3\omega^2LC+1}$$
$$z=\frac{(R+j\omega L)(1-3\omega^2LC-j3\omega RC)}{j3\omega RC(1-3\omega^2LC^2+(3\omega RC)^2}=\frac{R(1-3\omega^2 RC)+j\left[\omega L(1-3\omega^2 LC)-3\omega R^2C \right]}{j3\omega RC(1-3\omega^2LC^2+(3\omega RC)^2}$$

この式変形の最後の式の虚部が0となるような静電容量を導出します。
$$\omega L(1-3\omega^2 LC)-3\omega R^2C =0$$
$$C=\frac{L}{3(\omega^2L^2+R^2)}=\frac{16\times10^{-3}}{3(5^2+5^2)}\sim 1.1\times 10^{-4}\,\,\rm F$$

デルタ結線、スター結線、Ｖ結線、それぞれの電圧と電流の大きさと位相の関係がきちんと頭に入っていれば、
スムーズに計算できるようになっていきます。

三相交流の計算を習得するには、類似問題をたくさん解くのがよいと思います。
私も苦手ですが、いろんな問題を解いてどんどん慣れていきましょう。