H30 問08

＜画像クリックで拡大表示＞
問題はこちら

解説

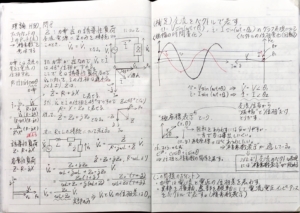
交流回路のインピーダンスに関する問題です。

力率、誘導性負荷というキーワードから\(\dot{Z}\)がどのような負荷なのかをイメージできないといけません。

力率は電圧と電流の位相差を表します。\(cos\theta=1/\sqrt{2}\)より位相差\(\theta\)は45°となります。そして、誘導性負荷なので、電圧に対して電流の位相が遅れます。

位相の遅れる/進むはそのまま覚えるだけだと間違えることがあります。
誘導性負荷の場合、\(\dot{Z}=R+jX\)、容量性負荷の場合\(\dot{Z}=R-jX\)を満たす（リアクタンス成分\(jX\)の正負が変わる）ことを覚えておきましょう。

以上の情報から\(\dot{Z}=Z_0+jZ_0\)（\(R=X=Z_0\)）となります。

次に、抵抗器\(R\)とコイル\(L\)を直列に接続し、\(\dot{Z}\)に印加される電圧\(\dot{V_2}\)を求めます。式変形をしていくと実部のみが残るため、\(\dot{V_1}\)と\(\dot{V_2}\)は同相、すなわち位相差は0であるということが分かります。

交流回路では、電圧と電流の大きさ（振幅）に加えて“位相差"も考えなくてはいけません。
位相差は電流/電圧またはインピーダンスをベクトルで表現することで、直感的に導出することができます。
しかし、交流をベクトルで表現するためには、複素数と極座標表示という数学的テクニックが必要になります。

（補足）で一応簡単な説明を記載していますが、これらの関係を理解しなくても大丈夫です。

交流回路をベクトルで表すには複素数を使うことだけ覚えておけば十分です。
横軸を実数、縦軸を虚数にして、ベクトルで表すということだけまず身に着けておきましょう。