H28 問03

＜画像クリックで拡大表示＞
問題はこちら

解説

ビオサバールの法則に関する問題です。

ビオサバールの法則は、公式を覚えても使い方が非常に分かりにくいです。
この計算には積分の知識が必要になるので、電験三種で難しい計算問題が出題されることはありません。

しかし、この問題のように計算方法を知らないと、回答できない問題は出題される可能性があります。

というわけで、ビオサバールの法則の考え方について解説していきます。

（１）電流が流れる経路の各点から渦が発生していると考える

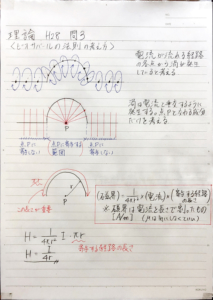
添付画像の上部のように電流経路の各点から渦が出ていると考えます。
渦は経路上の点を中心とした円で経路に垂直に発生しているとします。

（２）磁界の強さが知りたい任意の点Pについて、点Pと交わる渦の成分だけを考える

ビオサバールの法則は任意の点の磁界の強さを求めるために使用されます。
（ちなみに、アンペールの法則は電流（回路）が作るトータルの磁界の強さを求めるために使用されます）

ここで、ビオサバールの法則を適用する任意の点を点Pとすると、
電流経路と点Pの位置関係が重要になります。

点Pと交わる渦の成分のみが計算対象となります。
従って、この条件に当てはまらない部分は計算から除外できます。

点Pと交わらない渦の成分というのは言い換えると、電流の経路の延長線上に点Pがある部分です。
経路を伸ばして、点Pとぶつかるようならその部分は計算から除外できます。

この（２）の作業が最も重要です。
できるかぎり計算から除外できる部分を見つけないと、
ビオサバールの法則を使った計算はすごく複雑になります。

点Pと交わる渦の成分を抽出した結果、電流経路\(\pi r\)が計算に寄与する経路の長さとなります。

（３）磁界の計算を行う

ビオサバールの法則の一般化された公式は複雑なのですが、電験三種バージョンということで以下の公式を覚えておきましょう。

$$(磁界)=\frac{1}{4\pi r^2}\times (電流) \times (寄与する経路の長さ)$$

磁界、磁束、磁束密度など似たような物理量が磁気の分野にはたくさん登場しますが、
磁界とは電流を長さで割ったものです。（透磁率\(mu\)は不要です）

磁界の説明についてはいろいろな表現の仕方がありますが、余計なことは考えなくていいです。
「磁界とは電流を長さで割ったもの」この程度の理解で十分です。
（個人的な意見ですが、私は磁界と電束という2つの言葉があまり好きではありません。
これらの2つは物理現象を直感的に理解するうえで、あまり意味をなさないからです。）

計算を進めると、以下の結果が得られます。
$$H=\frac{1}{4\pi r^2}\cdot I \cdot \pi r = \frac{I}{4r}$$

分母が\(r\)の一乗になれば、OKです。
二乗や三乗になってしまったら、経路の式の設定が間違えている可能性が高いです。

ビオサバールの法則は、個人的には電磁気学の中でもっとも分かりにくい公式の一つだと思っています。

この解説を通じて、ビオサバールの法則の理解が深まれば幸いです。