H27 問08

＜画像クリックで拡大表示＞
問題はこちら

解説

交流回路の電力に関する問題です。

直流回路では、電力＝電流×電圧で求められます。
しかし、交流では、電流と電圧の間に位相差があるケースが存在します。

位相差があるということは複素平面上で、実部と虚部に分かれることになり、
その成分毎に名前が付けられています。

＜交流回路の電力＞
$$S=P+jQ$$
ここで、\(S\)は皮相電力、\(P\)は有効電力、\(Q\)は無効電力とそれぞれ呼ばれます。

馴染みがあるのは有効電力ですが、有効電力は抵抗で消費される電力、
または電流と電圧の内積（ベクトルで言うと同じ方向の成分の積）と表現されます。

まとめて、以下のようにイメージしてもらえばOKです。

有効電力＝（抵抗で消費される電力）＝（交流の電力の実部）＝（電流と電圧の同じ方向の成分）

続いて無効電力ですが、これは名前の通り無効となる電力です。
抵抗で消費される消費電力とは違い、コンデンサやコイルに蓄えられ、放出される電力です。

電源側から見ると、負荷に対してエネルギーを供給しているつもりが、タイミングがずれて電源に帰ってくる電力です。
この電力は実際に使われることはなく、電源と負荷の間で行ったり来たりする電力となります。

無効電力は複素平面で見ると、虚部の成分となります。

まとめると、以下のようにイメージしてもらえばOKです。

無効電力＝（コイルやコンデンサで一時的に蓄えられる電力）＝（交流の電力の虚部）

最後に皮相電力ですが、これは有効電力と無効電力を足したものです。
有効電力は実数と無効電力は虚数なのでベクトル和となることに気をつけましょう。

以上を踏まえて、解説に移ります。

問題では抵抗とコイルが直列に接続されているので、電流と電圧の間には位相差が生じます。

皮相電力＝有効電力とならないので、うまく皮相電力の実部の成分を抽出することを意識して計算を進めましょう。

電気回路では実軸上に電圧（電源）を設定することが多いですが、
電力を考えるときは電流を実軸上に設定するほうが計算しやすいです。

いろんな参考書で電流を実軸に設定して計算が行われていますが、
この説明はなしに、暗黙の了解で設定されています。
（これが交流の電力計算で躓く原因の一つだと私は思っています）

結論を先に言うと、\(P＝RI^2\)の関係式によりこの問題の解を求めることができます。

2行程度の式で完結しますが、なんでそうなるのかもやもやが残ると、
他の問題を解く力が身につかないので、少ししつこいと感じるかもしれませんが、
以下では細かい式の変換をしながら解を導出していきます。

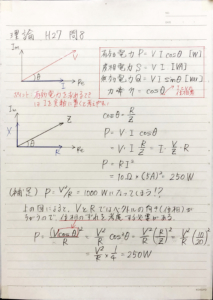
電流と電圧の位相関係を複素平面で表すと、添付画像の上部の図のようになります。
さらに抵抗\(R\)と誘導性リアクタンス（コイル）\(X\)のベクトルの関係を複素平面で表すと、
添付画像の中央部の図のようにあります。

2つの複素平面を眺めると、電流\(I\)と抵抗\(R\)が実軸上にあり、
電圧\(V\)とインピーダンス\(Z\)が同じ方向をむくベクトルであることが分かります。

このイメージをきちんと押さえておきましょう。

次に電力の計算のための式変形をしていきます。
先に説明したように、電流と電圧のベクトルの内積が有効電力になります。
そこから式変形をスタートしてきましょう。
$$P=V\cdot I \cos\theta =V\cdot I\cdot \frac{R}{Z}=I\cdot \frac{V}{Z}\cdot R=RI^2$$
ここで、\(\cos \theta=\frac{R}{Z}\)、\(V=ZI\rightarrow\,\frac{V}{Z}=I\)という関係式を使って式変形を行っています。

最初の宣言通り、\(P=RI^2\)の関係式が得られたので、\(R\)と\(I\)にそれぞれ値を代入すると、
$$P=RI^2=10\times5^2=250\,\,W$$
を導くことができます。

さて、ここで\(P＝V^2/R\)でも計算できるんじゃないと感じたあなた。

感がいいです。

しかし、\(P＝V^2/R\)では\(P＝1000W\)になってしまいます。
これこそが交流の電力の不思議なところなんです。

というわけで、補足として\(P＝V^2/R\)ではうまくいかないという解説を行います。

もう一度、添付画像の2つの複素平面を眺めてみましょう。

電圧と抵抗のベクトルの方向はどうなっていますか？

気づきましたか？抵抗は実軸上にいますが、電圧は違う方向を向いています。

ベクトルの方向が違うので、単純に電圧と抵抗の割り算をしてはいけません。

この場合、電圧のベクトルから実軸成分を取り出す必要があり、\(V\cos\theta\)として計算を行う必要があります。

ということで、式変形をしてみます。
$$P=\frac{(V\cos\theta)^2}{R}=\frac{V^2}{R}\cos^2\theta=\frac{V^2}{R}\left(\frac{R}{Z}\right)^2$$
ここで、\(Z=V/I=20\)をとなるので、値を代入すると、
$$P=\frac{V^2}{R}\left(\frac{10}{20}\right)^2=1000\times\frac{1}{4}=250\,\,W$$
となり、\(P=RI^2\)の結果と一致します。

交流の電力計算は、答えは導出できるけど、あっているかどうかよく分からないというケースが多いです。

そういう状況に陥る理由は、電流と電圧の位相差を常に意識しないといけないからです。

・電流と電圧の位相を複素平面に描く
・インピーダンスの実部と虚部を複素平面に描く

この2つの作業を習慣づけて電力の計算を行えば、交流回路の下地がしっかりと身につくはずです。
慣れるまでは大変ですが、是非試していただきたいです。