H27 問10
<画像クリックで拡大表示>
問題はこちら
解説
電気回路の過渡応答に関する問題です。
スイッチを閉じた瞬間の電流と電圧の振る舞いは、コイルとコンデンサで異なります。
この問題を機にその特徴を押さえておきましょう。
いろいろな解釈の仕方がありますが、一番とっつきやすいのは、
交流回路のインピーダンスの式にω=∞を代入した状態がスイッチを閉じた瞬間のインピーダンス
と考えることだと思います。
コイルのインピーダンスは、
$$R_L=j\omega L$$
と表せるので、\(\omega =\infty\)では\(R_L=\infty\)となります。
コンデンサのインピーダンスは、
$$R_C=\frac{1}{j\omega C}$$
と表せるので、\(\omega =\infty\)では\(R_C=0\)となります。
直流回路ではスイッチをONにした瞬間、コイルは開放(オープン)、コンデンサは短絡(ショート)
として振る舞うということを押さえておきましょう。
このイメージを頭において問題を解いていきます。
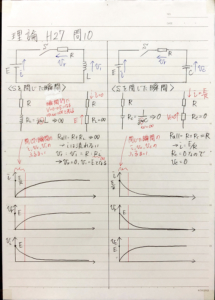
RL回路のスイッチを閉じた瞬間
スイッチを閉じた瞬間、コイルのインピーダンスは\(R_L=\infty\)となるので、電源電圧は全てコイルに印加されます。
従って\(v_i=E\)となります。
一方、抵抗\(R\)の電圧は\(v_r=E-v_i\)となるので、\(v_r=0\)からスタートします。
電流\(i\)は、\(R_L=\infty\)なので\(i=0\)からスタートします。
コイルのインピーダンスは時間経過とともに徐々に小さくなり、最終的に\(R_L=0\)になります。
コイルは電流が変化しようとするときに逆向きに誘導電圧を発生させる特性(ファラデーの法則)があり、
スイッチを閉じた瞬間に大きな誘導電圧が発生しますが、
その後電流の変化は緩やかになり、誘導電圧も小さくなっていくからです。
ということで、コイルのインピーダンス\(R_L\)が小さくなるにつれて、抵抗の電圧\(v_r\)が大きくなり、電流\(i\)も大きくなります。
以上がRL回路の過渡応答となります。
RC回路のスイッチを閉じた瞬間
スイッチを閉じた瞬間、コンデンサのインピーダンスは\(R_C=0\)となるので、電源電圧は全て抵抗に印加されます。
従って\(v_C=0\)、\(v_r=E\)となります。
電流\(i\)は\(i=E/R\)からスタートします。
コンデンサに電流が流れるとコンデンサ内に電荷として蓄えられ、\(V_C=Q/C\)の電圧が発生します。
その結果、抵抗の電圧\(V_r\)が徐々にちいさくなり、電流\(i\)もつられて小さくなります。
\(V_C=E\)に達すると、電源電圧は全てコンデンサに印加されることになり、\(V_r=0\)、\(i=0\)となります。
以上がRC回路の過渡応答となります。
従って、この問題の答えは(2)となります。
コイルとコンデンサの過渡応答の基本的な情報をまとめた問題なので、
苦手意識のある方は、この問題を活用して要点を押さえておきましょう。





