H28 問13

＜画像クリックで拡大表示＞
問題はこちら

解説

トランジスタを含む回路に関する問題です。
しかし、トランジスタに関する知識は不要です。

この問題は電圧利得とデジベルという言葉を理解しているかどうかにかかっています。

電圧利得とは

電圧利得は入力電圧に対する出力電圧の増幅率を意味します。
（電圧利得）＝（出力電圧）/（入力電圧）
と表せます。

そして、単位がデジベルの場合、以下のように表現します。
$$A_v=20\log_{10}\left|\frac{v_o}{v_i}\right|$$

式を説明するよりも、以下の関係を見るほうがデジベルのイメージがしやすいと思います。
0dB → 1倍（\(v_o=v_i\))
3dB → \(\sqrt{2}\)倍（\(v_o=\sqrt{2}v_i\))
20dB → 10倍（\(v_o=10v_i\))
40dB → 100倍（\(v_o=100v_i\))
100dB → 10,000倍（\(v_o=10,000v_i\))

電圧利得が10倍より大きいと、10倍ごとにデジベルの値が20ずつ増えていくのが分かります。
入力信号と出力信号が桁違いに大きい/小さい場合に使い勝手がいい単位となります。

「デジベル表示は桁違い」

と覚えましょう。

解の導出

電圧利得とデジベルの役割が分かったので、計算を進めます。

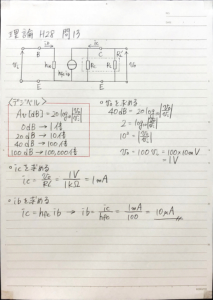
（１）\(v_o\)を求める
電圧利得は40dBなので、
$$v_o=100v_i=100\times 10mV=1V$$
となります。

（２）\(i_c\)を求める
\(R_C\)と\(R_L\)をまとめて\(R_L’\)としているのでこの負荷を利用して、オームの法則より、
$$i_c=\frac{v_o}{R_L}=\frac{1V}{1k\Omega}=1mA$$

（３）\(i_b\)を求める
\(i_b\)と\(i_c\)の関係は問題の回路図より、
$$i_c=h_{fe}i_b　\rightarrow i_b=\frac{i_c}{h_{fe}}=\frac{1mA}{100}=10uA$$
となります。

デジベルという単位は、オーディオ向けの電子回路や高周波回路くらいしか使うことはないですが、
ボルトやアンペアよりも一般に普及している単位です。
これを機に覚えておくのもよいと思います。

参考になれば幸いです。