H29 問16

＜画像クリックで拡大表示＞
問題はこちら

解説

三相交流回路に関する問題です。

三相交流回路はデルタ結線とスター結線があります。
そして、変換やその他公式をみるといろんなところに\(\sqrt{3}\)やら\(3\)やら\(1/\sqrt{3}\)がついて、
ちゃんと覚えるのに苦労します。
（私はちょっと時間が経ったらすぐに忘れてしまいます。）

とにかく、電源のデルタースター変換だけは覚えておきましょう！
デルタからスターへの変換は\(1/\sqrt(3)\)倍
スターからデルタへの変換は\(\sqrt{3}\)倍
です。

どっちがどっちか分からなくなるという人は、とにかくデルタからスターへの変換は\(1/\sqrt(3)\)倍
だけ覚えてください。

困ったら、スター結線に変換する。そのときは\(1/\sqrt(3)\)倍する。
この気持ちがあれば、スター結線があなたを答えに導いてくれます。
（少なくともこの記事を書いている2019年12月の段階では私はそう信じています）

では、スター結線を信じて解説を進めていきます。

設問(a)について

まず力率について考えていきますが、電源を無視して負荷のみで導出が可能です。
幸い、負荷側の回路はスター結線になっているので、変換は行いません。

力率とは、負荷の実部成分の割合になります。\(R/|\dot{Z}|\)を求めればよく、
\(\frac{R}{|\dot{Z|}}=\frac{R}{\sqrt{R^2+(2\pi fL)^2}}=0.95\)となります。

次に有効電力を導出します。

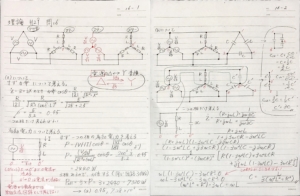
電源回路がデルタ結線になっているので、ここでデルタースター変換の登場です。
回路図を描くと、添付画像の左上から右上の図のように変換ができます。

スター結線にすると何がいいかというと、
三相のそれぞれの回路の電流が全て中点で合流し、その合計が0になることです。

電源から負荷の出口（図中の中点\(O’\)まで）を1つの閉じた回路と考えてよく、
中点で電流が0になるので、
他の相の回路の負荷の大きさや、他の相の回路から流れ込んでくる電流を気にしなくていい
というのが三相交流回路の魅力的なところです。

その結果、スター結線にしてしまえば、同じ回路が3つあると考えればいいので、
とりあえず1つの相について計算をして、
あとは3倍すればOKというアプローチで解を求めることができます。

というわけで、まず1つの相の有効電力を求めます。

有効電力は\(P=\frac{|\dot{V}|^2}{|\dot{Z}|}cos\theta\)より求めることができ、\(P=2440W\)となります。
次に三相分の電力にするには、回路3つ分の合計つまり3倍すればいいことになり、
\(P_{all}=3\times P = 7320W\)が導出でき、最も近い\(7.28\times 10^3 W\)が解となります。