H30 問16

＜画像クリックで拡大表示＞
問題はこちら

解説

トランジスタを含む電子回路に関する問題です。

トランジスタの動作原理を抑えつつ、周辺回路の電流/電圧をオームの法則やキルヒホッフの法則を用いて決定していくことになります。

電験3種の電気回路の問題では、最高難度の問題だと思います。
きちんとポイントを押さえながら、計算をしていきましょう。

まず、動作点を問われている問題なので、”直流”成分だけ考えればOKです。
交流電源やコンデンサが回路接続されていますが、一切無視してかまいません。

それを踏まえて、\(V_{CC}\)を電源とした回路の部分に注目し、エミッタ電流\(I_E\)を求めていきます。
トランジスタのエミッタ電流\(I_E\)は以下の手順で求めていきます。

電源\(V_{CC}\)に対して、抵抗\(R_1\)、\(R_2\)とトランジスタは並列に接続されていると考えてかまいません。
（\(R_1\)、\(R_2\)の間にベース端子が接続されていますが、気にしなくていいです）

従って、ベース電圧\(V_B\)は\(R_2\)に印加される電圧を考えればいいので、

\(V_B=\frac{R_2}{R_1+R_2}V_{CC}\)となります。

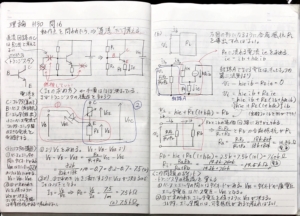
添付の画像にトランジスタの構造が示してあります。（左のページの中央部分）

この画像を見ると、トランジスタのベースーエミッタ端子間には、ダイオードが順方向に接続されています。
トランジスタの動作を説明するにあたり、このダイオードの働きがすごく重要になってくるので、
ベースーエミッタ間にダイオードがあるということは覚えておきましょう。

問題でも\(V_{BE}=0.7V\)という条件が与えられています。実はこの電圧はダイオードに印加される電圧を表しています。

先ほど、ベース電圧\(V_B\)を求めたので、\(V_E=V_B-V_{BE}\)の関係から、エミッタ電圧\(V_E\)を求めることができます。

\(V_E=V_B-V_{BE}=\frac{R_2}{R_1+R_2}V_{CC}-V_{BE}\)となります。

３．エミッタ電圧\(V_E\)とエミッタ抵抗\(R_E\)よりエミッタ電流\(I_E\)を求める

先に求めたエミッタ電圧\(V_E\)を用いて、エミッタ電流\(I_E\)を求めることができます。
問題では、エミッタ電流\(I_E=1mA\)とするためのエミッタ抵抗\(R_E\)の値を求められているので、
\(R_E =V_E/I_E\)の関係を用いて、エミッタ抵抗\(R_E\)を導出します。

さて、ここまで一切説明をされず、出番もなかったコレクターエミッタ間電圧\(V_{CE}\)について、少し解説をしたいと思います。

実はエミッタ電流\(I_E\)を求めるには、\(V_{CE}\)は考えなくてもいいんです。
正確には、\(V_{CE}\)は考えなくてもいいように\(V_{CE}\)の値は勝手に決まっています。

この\(V_{CE}\)の動作にこそ、トランジスタの面白い特性が隠されています。

ベース電圧\(V_B\)とエミッタ電圧\(V_E\)によりエミッタ電流\(I_E\)が決まると、
\(V_{CE}=V_{CC}-V_E\)の関係を満たすように\(V_{CE}\)の値が決まります。

この問題では\(V_{CC}=10V\)、\(V_E=7.5V\)と設定されているので、\(V_{CE}=2.5V\)となります。
例えば、\(V_{CC}=100V\)、\(V_E=7.5V\)となるように回路を変更すると、\(V_{CE}=92.5V\)となります。

\(V_{CE}\)がエミッタ電流\(I_E\)に合わせて変動するというこの特性が、
トランジスタが電流や電圧の制御に広く使われていることにつながっています。

問題の図２は図１のトランジスタ部分の等価回路を表しているわけですが、
そんなことは気にせず、入力インピーダンスと定義された\(R_i=v_i/i_i\)を導出していきます。

図２の回路には電流源\(h_{fe}i_{b}\)が含まれているので、この部分の取り扱いには注意が必要です。

電流源は決まった電流を回路に供給することが目的です。
オームの法則とは別のルールを回路に設定していると思って、計算を進める必要があります。

そのために、まず電流源\(h_{fe}i_{b}\)が影響する部分の計算を行います。
電流源\(h_{fe}i_{b}\)はエミッタ抵抗\(R_E\)に電流を供給します。

エミッタ抵抗\(R_E\)には電流源\(h_{fe}i_{b}\)と\(i_b\)が接続されるので、
\(i_e=h_{fe}i_{b}+i_b\)と表わすことができます。

次に添付の画像の経路Aの部分で生じる電圧をキルヒホッフの第二法則で表します。
（添付の画像の右のページ中央付近です）

式変形を進めていくと、\(v_i=[h_{ie}+R_E(1+h_{fe})]i_b\)と表せます。
この式は[定数]\(\times i_b\)の形になっているので、[定数]\(=R_b\)とし、
抵抗\(R_b\)に\(i_b\)が流れていると考えることができます。

さらに\(R_b\)は抵抗\(\frac{R_1R_2}{R_1+R_2}=R_a\)に並列に接続されています。

従って、\(R_i=\frac{R_aR_b}{R_a+R_b}\)の関係から入力インピーダンス\(R_i\)を導出することができます。

すごく情報量の多い解説になってしまいましたが、
エミッタ電流\(I_E\)の求めるための3つのポイントと\(V_{CE}\)の特性を合わせて、
以下4つのポイントがトランジスタを含む電子回路では重要になります。

これらのポイントを確認しながら、類似問題を解いてテクニックを習得していきましょう。