H29 問10

＜画像クリックで拡大表示＞
問題はこちら

解説

コイルを含む直流回路の過渡応答に関する問題です。

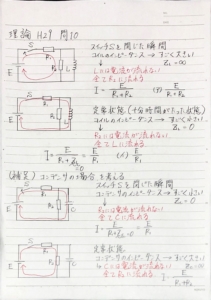
スイッチSを閉じた瞬間と定常状態（十分時間がたった状態）で
コイルのインピーダンスが変化することがポイントです。

スイッチSを閉じた瞬間：コイルのインピーダンス　大（$Z_L = \infty$）
定常状態：コイルのインピーダンス　小（$Z_L = 0$）

スイッチSを閉じた瞬間は$Z_L = \infty$となるので、
コイルには電流が流れず、全て$R_2$に流れます。

定常状態では$Z_L = 0$となるので、
$R_2$には電流が流れず、全てコイルに流れます。

電流の経路さえ分かれば、あとはオームの法則で
それぞれの条件の電流を求めることができます。

補足として、添付画像の下部で
コイルをコンデンサに置き換えた場合について解説しています。

コンデンサのインピーダンスは以下のように変化します。

スイッチSを閉じた瞬間：コンデンサのインピーダンス　小（$Z_C = 0$）
定常状態：コンデンサのインピーダンス　大（$Z_C = \infty$）

スイッチSを閉じた瞬間は$Z_C = 0$となるので、
$R_2$には電流が流れず、全てコンデンサに流れます。

定常状態では$Z_C = \infty$となるので、
コンデンサには電流が流れず、全て$R_2$に流れます。

スイッチを閉じた瞬間のインピーダンスの振る舞いはコイルとコンデンサで真逆の特性になります。

時間による電流や電圧の変化を過渡応答と言います。

数式を使ってその特性を計算することはできますが、
時間に対する素子の振る舞いを直感的にイメージできることのほうが大切です。

イメージができると計算をしなくても電気回路の動作が分かるようになってきますので、
過渡応答が苦手な方は何度か問題を解いてテクニックを習得してください。