H28 問06

＜画像クリックで拡大表示＞
問題はこちら

解説

直流の電気回路に関する問題です。

電流$I_1$と$I_2$の電流比を求める問題です。

電圧や合成抵抗なんて、全く気にしなくて構いません。

並列回路の電流比は抵抗の逆比　で決まる。

ただ1つの条件だけを使って解を導出していきます。

以下のアプローチで計算を進めます。

並列部の抵抗値が分かっているので、電流$I_2$と$I_2’$の比は以下のようになります。
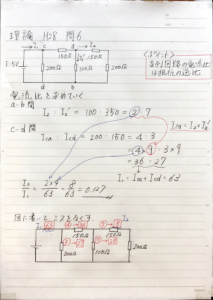
$$I_2 : I_2′ =100 : 350 = 2 : 7$$

１と同様に並列部の抵抗値が分かっているので、電流$I_{ca}$と$I_{cd}$の比は以下のようになります。
$$I_{ca} : I_{cd} =200 : 150 = 4 : 3$$

a-b間の電流比を4倍、c-d間の電流を9倍すると、全体の電流比が求められます。
添付画像の一番下の図のように、各電流の比率を全て図に記載するのがよいと思います。

以上より、電流$I_1$と$I_2$の電流比は、
$$\frac{I_2}{I_1}=\frac{2\times 4}{63}=0.127$$
となります。

複数の並列回路で構成される直流回路の計算では、各部の抵抗さえ分かっていれば、この問題のように回路全体の電流比が分かります。
電流比が分かると、回路全体の電流分布が把握できるので、その回路の動作がイメージしやすくなります。

回路設計者にとっては欠かせないテクニックであり、計算が短縮できるので電験向けだと思います。

是非参考にしてください。