R01 問01

＜画像クリックで拡大表示＞
問題はこちら

解説

点電荷が作る電位に関する問題です。
以下の公式を知っていれば、簡単に解を導出することができます。
$$V_{AB}=\frac{Q}{4\pi \varepsilon_0}\left( \frac{1}{x_A}-\frac{1}{x_b}\right) $$
（ここでは問題と合わせてBが始点、Aが終点となるようにしています。）

電位を求めることよりも、電界と電位の関係を理解しておくことが重要です。
以下では、この電位の式を用いた解法と電界の式を用いた解法の2つを解説していきます。

解法１）電位の式から求める

問題の実験内容で(a)から(d)の各条件で、点Aと点Bの位置が設定されています。
点Pの位置を0mとしてそこから、点Aと点Bの位置を導きます。

条件(a)では、点Aの位置\(x_A=2m\)、点Bの位置\(x_B=3m\)となります。
電位の式に\(x_A=2m\)、\(x_B=3m\)を代入すると、
$$V_{AB}=\frac{Q}{4\pi \varepsilon_0}\left( \frac{1}{2}-\frac{1}{3}\right)= \frac{Q}{4\pi \varepsilon_0}\left( \frac{1}{6}\right)$$
が得られます。

同様の手順で各条件の電位を求めていきます。

条件(b)では、点Aの位置\(x_A=1m\)、点Bの位置\(x_B=3m\)となり、
$$V_{AB}=\frac{Q}{4\pi \varepsilon_0}\left( \frac{1}{1}-\frac{1}{3}\right)= \frac{Q}{4\pi \varepsilon_0}\left( \frac{2}{3}\right)$$
が得られます。

条件(c)では、点Aの位置\(x_A=0.5m\)、点Bの位置\(x_B=1.5m\)となり、
$$V_{AB}=\frac{Q}{4\pi \varepsilon_0}\left( \frac{1}{0.5}-\frac{1}{1.5}\right)= \frac{Q}{4\pi \varepsilon_0}\left( \frac{4}{3}\right)$$
が得られます。

条件(d)では、点Aの位置\(x_A=1m\)、点Bの位置\(x_B=1.5m\)となり、
$$V_{AB}=\frac{Q}{4\pi \varepsilon_0}\left( \frac{1}{1}-\frac{1}{1.5}\right)= \frac{Q}{4\pi \varepsilon_0}\left( \frac{1}{3}\right)$$
が得られます。

各条件より得られた電位の値から、最小の条件は(a)、最大の条件は(c)が解となります。

解法２）電界の式とグラフから求める

電位の式は知らなくても、電験三種で出題頻度の高い電界の式は覚えているという方は多いと思います。
以下が点電荷が作る電界の公式です。
$$E(x)=\frac{Q}{4\pi\varepsilon_0}\frac{1}{x^2}$$

この電界の式を使って、グラフを描き、そこから電位を求めることができます。

ポイントは、”点Aから点Bまでの範囲の電界の面積が電位を表している”ということです。

グラフは簡単なものでかまいません。公式の\(\frac{Q}{4\pi\varepsilon_0}\)は無視して、
\(y=\frac{1}{x^2}\)のグラフが描ければ十分です。

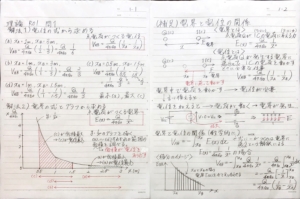
添付画像を参考にしてグラフを描いてみましょう。
そして、各条件の点Aと点Bの範囲での\(y=\frac{1}{x^2}\)での面積を調べます。
面積の計算はしなくて構いません。\(y=\frac{1}{x^2}\)がきちんと描ければ、面積は目分量で十分です。

添付画像のグラフの赤色斜線の部分が条件(c)の電界の面積を表して、この条件が最も面積が大きくなります。
緑色斜線の部分が条件(a)の電界の面積を表して、この条件が最も面積が小さくなります。

条件(b)もそこそこ面積が大きく、(c)より大きいんじゃないかと思う方もいるかもしれません。
グラフを見やすくするために、縦軸に対して横軸の縮尺を2倍に設定した私のミスです。
気になる方は、縦軸と横軸の縮尺を同じにしてグラフを描いてみてください。

繰り返しになりますが、（電界の面積）＝（電位）という部分がポイントです。
数学的な言葉で表現すると、電界の積分が電位となります。

電験三種の問題では微分積分を用いた計算は要求されません。
しかし、電磁気のイメージを身につけるために微分積分の知識は必ず必要になります。

小難しいことは置いておいて、なんとなく積分のイメージが分かるように、
補足として、電界と電位の関係の解説をしていきます。（添付画像の右のページ）

電界とは、点電荷Qが1C（クーロン）の電荷に与える力です。

そして、電位とは、点電荷Qが発生する電界に逆らって1Cの電荷を動かすときに必要な仕事です。

従って、電界中で電位を動かすには電位が必要になります。

言い換えると、電位を加えると、電荷が動き、電界が発生します。
平行板の電極間に電位を印加すると、電極間で電界が発生するのは、まさに電界と電位の関係を表しています。

また、電界は力、電位は仕事を表しているということがポイントになります。

仕事とは、外力（重力やバネの引っ張り力）などに逆らって、物体をある距離だけ動かすときに
必要な力の総和のことを言います。

かみ砕いていうと、例えば１ｍ物体を動かす場合、１ｍｍごとに力が必要になるので、
それを全部足し合わせたものが仕事です。

この１ｍという範囲の中で、１ｍｍという小さな刻みで値を足し続けるという行為が、積分になります。

数式で表すと以下のようになります。
$$V_{AB} = – \int_{x_A}^{x_B}E(x)dx= – \int_{x_A}^{x_B}\frac{Q}{4\pi\varepsilon_0}\frac{1}{x^2}dx$$
$$ = – \frac{Q}{4\pi\varepsilon_0}\int_{x_A}^{x_B}\frac{1}{x^2}dx=-\frac{Q}{4\pi\varepsilon_0}\left[-\frac{1}{x}\right]_{x_B}^{x_A}$$
$$V_{AB} =-\frac{Q}{4\pi\varepsilon_0}\left(\frac{1}{x_A}-\frac{1}{x_B}\right)$$

電界と電位の公式を比べると、なんとなく似ているなと印象はあると思います。
分母が\(1/x^2\)か\(1/x\)かの違いだけです。

しかし、その違いをはっきりさせるためにそれぞれの物理的な意味を理解し、
数式を用いて結びつけてあげる必要があります。

問題を解けるようになることと、本質を理解をすることの間の大きな隙間はここにあります。
電気の”なんで？”を解消していくためには、たくさんの予備知識が必要です。

全てを一度に理解する必要はありません。
いろんな問題を解いていき、ときどきこの解説を見直してみて、
理解できればラッキー、難しいと感じたらまた今度というくらいの軽い気持ちで、
少しずつ理解を深めていければよいと思います。

この解説が、電界と電位の理解に役立てば幸いです。