R01 問16

＜画像クリックで拡大表示＞
問題はこちら

解説

三相交流に関する問題です。

設問（ａ）

電源電流\(I\)を求めます。

問題で与えられる回路は電源、負荷ともにスター型になっているので、回路の変換は不要です。

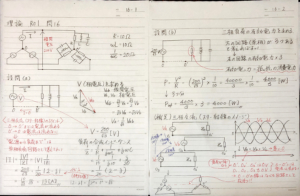
スター型になっているので、一相分だけ回路を取り出して、計算を進めます。（添付画像の左ページの中央部分）

しかし、電源電圧として与えられる情報は”線間電圧”なので、このままではうまく使えません。
そのため、一相分の回路の電源電圧（相電圧）になるように変換が必要です。

線間電圧と相電圧の関係は、添付画像の左ページの中央部分（右側）に記載しています。

各相の電源電圧（相電圧）は120°ずつ位相が回転しています。
線間電圧は2つの相電圧のベクトル和で表すことができるので、
ベクトル図を描くことで、それぞれの大きさと位相差の関係を紐解くことができます。

ここではとりあえず大きさの関係が分かればよく、
（相電圧）＝\(1/\sqrt{3}\)×（線間電圧）
の関係を使って計算を進めていくと、電源電圧\(V=200/\sqrt{3}\)が得られます。

電源電流\(I\)を求めるために、合成インピーダンスを求めます。
$$\frac{1}{Z}=\frac{1}{R}+\frac{1}{j\omega L}+j\omega C$$
並列回路のインピーダンスの計算は複雑なるので、さらに式変形をしていくか悩ましいのですが、
そういうときは一旦計算を止めて、他の計算を進めてみます。

電流と電圧の関係を考えると、\(I=V/Z\)となります。
この式ではインピーダンスは\(1/Z\)の形で使用するので、合成インピーダンスは\(1/Z\)の形で式変形を進めていきます。

先の合成インピーダンスの式に、\(R=10\Omega\)、\(\omega L =10\Omega\)、\(1/\omega C=20\Omega\)を代入します。
$$\frac{1}{Z}=\frac{1}{10}+\frac{1}{j10}+\frac{j}{20}=\frac{1}{20}\left( 2-j\right)$$

電源電圧とインピーダンスの大きさが得られたので、電流を導出します。
$$|I|=|V|\cdot\frac{1}{|Z|}=\frac{200}{\sqrt{3}}\cdot\frac{1}{20}\cdot|2-j|=\frac{10}{\sqrt{3}}\sqrt{5}=13[A]$$

設問（ｂ）

三相負荷の有効電力を求めます。
スター型の回路で計算を行っているので、一相分の消費電力を求めて、3倍すれば三相負荷の有効電力となります。

また有効電力とは抵抗で消費される電力です。
設問（ａ）で抵抗の値と印加される電圧の値は分かっているので、以下のように計算ができます。
$$P=\frac{V^2}{R}=\left(\frac{200}{\sqrt{3}}\right)^2\cdot\frac{1}{10}=\frac{4000}{3}[W]$$
ここで求めたのは一相分の有効電力なので3倍すると、
$$P_{3\phi}=4000[W]$$
となります。

補足では、三相交流（主にスター結線）のイメージについての解説をつけてみました。

スター結線では同じ回路が3つあると考えてよいということ、
負荷から電源へ電流が戻るルートは0V/0Aになるので、負荷より先の電圧や電流は気にしなくていいということ、

この2つが身につけば、三相交流の苦手意識は少なるはずです。

参考になれば幸いです。