R01 問18

＜画像クリックで拡大表示＞
問題はこちら

解説

AD変換器の原理に関する問題です。

AD変換器とはアナログ信号をデジタル信号に変換する機能をもつ電気回路のことを言います。

アナログ信号というのは、電験で扱われる電子回路や電気回路のことで、
デジタル信号とはコンピュータで処理ができるデータのことを言います。

つまり、電気回路で得た情報をコンピュータで処理するための仲介の役割をするのがAD変換器です。

AIやIoTなどデータ処理の技術やCPUの発達で、ソフトウェアでできることがどんどん増えています。
そして、IC（集積回路）の発達でハードウェアはどんどん小型化、パッケージ化されています。

反面、電気回路や電子回路の基本概念はすでに完成しており、レガシーな技術となっています。

しかし、アナログ信号からデジタル信号の変換、すなわちAD変換は絶対に無くなりません。
そして、この部分の設計こそ電気設計者にとってのキー技術であり、
電気回路や電子回路の歴史を作ってきた先代の技術者から継承していくべき技術となっています。

少し熱くなってしまいましたが、電気施設管理者を目指し電験の学習をしている皆様に、
電気設計者の価値を知っていただきたく、このようなコメントを記載させていただきました。

というわけで、AD変換は電気設計者にとってすごく大切な技術です。
ですので、この問題を通じてAD変換というものを知ってもらえれば幸いです。

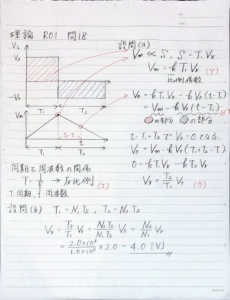
設問（ａ）

二重積分型AD変換器の特徴は、積分を利用してAD変換を行うことです。

「積分」という言葉が苦手な方もいるかと思いますが、
要は決まった期間（時間）の間、値を足し続けるのが積分です。

まず、入力信号（未知電圧$V_x$）を決まった時間$T_1$の間、積分し続けます。
具体的には、電圧に比例した電流でコンデンサに充電を行います。
コンデンサの電圧は$Q=CV$すなわち$It=CV$で決まります。
電流によりコンデンサに電荷がたまり、時間に比例して電圧が増えていきます。

コンデンサがバケツ、電流が水と考えるとイメージしやすいと思います。
入力信号に応じた量に水が流れるとします。
人が制御できるのは水を流すか止めるかだけだとすると、決まった時間だけバケツに水がたまります。

今度は、コンデンサから放電を行います。電流の値を固定にすることで、時間に比例して電圧は小さくなっていきます。
この時、電荷がなくなる時間を測定すれば、コンデンサの容量と放電する電流の値をもとに、
入力信号（未知電圧$V_x$）の値を見積もることができます。

コンデンサのバケツの底に、蛇口がついていて、蛇口のひねり具合を固定することで、水の流量をコントロールできます。
バケツの中の水がなくなるまでの時間を測定すれば、入力信号を求めることができます。

このとき、バケツに水をためる時間とバケツから水を抜く時間は０、１、２・・・秒という決まった時間（時計の秒針）
みたいなもので制御することで、バケツの水が１．０、１．１、１．２・・・リットルという離散的な値で表すことができ、結果として入力信号が離散的な（デジタル）値に変換することができます。

この時の時間刻みを標本化（サンプリング）、入力信号が離散化されることを量子化と言います。

以上を踏まえて、問題の解答に移ります。

入力信号をもとにバケツに水をためる作業は
$$V_m=kT_1V_x$$
と表せます。

バケツから水を抜いている間のバケツの水の量（水位）は、
$$V_O=V_m-kV_r(t-T_1)$$
と表せます。

バケツから水がなくなる時間をもとに入力信号を求めると、
$$V_x=\frac{T_2}{T_1}V_r$$
と表せます。

ここで周波数と周期は反比例の関係となることはきちんと押さえておきましょう。

前問の$T_1$と$T_2$を標本化します。サンプリング周期$T_s$とクロックパルスの数を用いて、以下のように解を求められます。
$$V_x=\frac{T_2}{T_1}V_r=\frac{T_sN_2}{T_sN_1}V_r=\frac{N_2}{N_1}V_r=4.0[V]$$

この問題は、計算自体はそれほど難しくないのですが、
AD変換器の原理に触れていただきたく、細かく解説させていただきました。

この問題をきっかけにAD変換器の理解が深まれば幸いです。